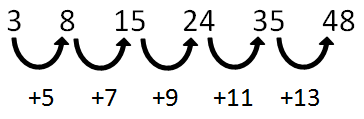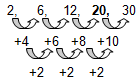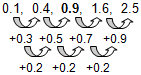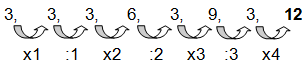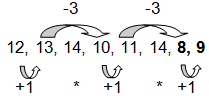Cijferreeksen oefenen op elk niveau
Wil je cijferreeksen oefenen voor je assessment of capaciteitentest? Daar helpen we je graag bij. Op deze pagina:
- krijg je uitleg over cijferreeksen;
- oefen je met 3 gratis testsimulaties op MBO, HBO en WO-niveau;
- ontvang je tips voor het oplossen van bekende en moeilijke cijferreeksen;
- ontdek je welke soorten cijferreeksen je kunt verwachten op je assessment.
Direct cijferreeksen oefenen? Klik hieronder op de (gratis) test die past bij het niveau van de opleiding of functie waar je voor solliciteert. 👇
Wil je daarna nog meer oefenen? Gebruik dan ons Cijferreeksen oefenpakket, inclusief honderden oefenvragen op elk niveau, tientallen realistische testsimulaties onder tijdsdruk en handige uitleg- en scorerapporten.
Cijferreeksen oefenpakket
Dit Cijferreeksen oefenpakket bevat:
- 450+ oefenvragen (MBO, HBO en WO-niveau)
- 10+ realistische simulaties onder tijdsdruk
- Voorbereiding op cijferreeksassessments van LTP, GITP, Assessio, Talent Q en meer
- Uitgebreide uitleg, antwoorden en tips per vraag
- Persoonlijk scoreoverzicht na elke test
- Beschikbaar in zowel Nederlands als Engels
- 100% online, op alle apparaten te gebruiken
Wat zijn cijferreeksen?
Een cijferreeks is een reeks getallen die volgens een logisch patroon is opgebouwd. Eén of meerdere getallen ontbreken en het is aan jou om te bepalen welk getal daar logisch hoort. Een bekend voorbeeld:
Voorbeeld van een bekende cijferreeks
Welk getal hoort op de plek van het vraagteken?
1, 2, 4, 8, 16, ?
Klik op het juiste antwoord:
Natuurlijk zijn lang niet alle reeksen zo eenvoudig. In moeilijke cijferreeksen veranderen de tussenstappen, lopen er twee patronen door elkaar of is het patroon gebaseerd op kwadraten, breuken of vermenigvuldigingen.
Daarom is het belangrijk om verschillende soorten cijferreeksen te leren herkennen en te weten hoe je ze efficiënt oplost.
Hoe los je cijferreeksen op?
Bij het oplossen van cijferreeksen draait het om één vraag: wat is het patroon achter de reeks? Zodra je dat hebt ontdekt, kun je het ontbrekende getal(len) meestal vrij eenvoudig invullen. Zo pak je dat aan:
- Werk van links naar rechts. Bekijk steeds twee opeenvolgende getallen en check wat er gebeurt: optellen, aftrekken, vermenigvuldigen of delen.
- Let op het verschil van het verschil. Zie je geen duidelijk patroon? Kijk dan naar de verschillen tussen de verschillen. Dat onthult vaak een verborgen structuur.
- Controleer of het patroon wisselt. Sommige reeksen bestaan uit twee afwisselende subreeksen. Bekijk bijvoorbeeld de getallen op even en oneven posities afzonderlijk van elkaar.
- Let op de positie van het ontbrekende getal. Staat het getal aan het begin van de reeks? Dan heb je minder informatie en wordt het oplossen lastiger. Werk dan terug van achter naar voren.
- Gebruik kladpapier en noteer de stappen tussen de getallen. Door op te schrijven wat er verandert (bijv. +3, ×2), zie je sneller welk patroon erachter zit.
- Herken het type reeks. Hoe vaker je oefent met verschillende soorten cijferreeksen – zoals machtsverhoudingen of Fibonacci-reeksen – hoe sneller je ze tijdens een test herkent en oplost.
Bekijk hieronder hoe je de meest voorkomende soorten cijferreeksen oplost, inclusief uitleg en voorbeelden:
Een rekenkundige reeks is de eenvoudigste soort cijferreeks. Elk getal ontstaat door steeds hetzelfde getal op te tellen of af te trekken. Denk aan vaste stappen van bv. +2 of -5.
Zo herken je een rekenkundige reeks:
- Het verschil tussen twee opeenvolgende getallen is steeds gelijk.
- Het patroon zit in de afstanden tussen de getallen, niet in verhoudingen of vermenigvuldigingen.
Zo los je een rekenkundige reeks op:
- Trek twee opeenvolgende getallen van elkaar af om het verschil te berekenen.
- Controleer of dit verschil tussen alle getallen in de reeks gelijk blijft.
- Tel dat verschil op bij het laatste bekende getal om het volgende getal te vinden.
Enkele voorbeelden:
Eerste voorbeeld van een rekenkundige cijferreeks
Welke getallen horen op de plek van de vraagtekens?
1, ?, 5, ?, 9, 11
Klik op het juiste antwoord:
Tweede voorbeeld van een rekenkundige reeks
Welk getal hoort op de plek van het vraagteken?
1 | 1/2 | 3/9 | 5/20 | ?
Klik op het juiste antwoord:
Tip voor rekenkundige reeksen
Check het verschil niet alleen tussen de eerste twee getallen, maar tussen meerdere opeenvolgende stappen. Sommige reeksen beginnen als een rekenkundige reeks, maar bouwen later extra stappen in, zoals een afwisselend verschil of een dubbele logica. Door het verschil op meerdere plekken te controleren, voorkom je dat je te vroeg een patroon aanneemt dat niet klopt.
In een meetkundige reeks wordt elk getal gevormd door het vorige getal te vermenigvuldigen of te delen met een vast getal. Denk aan een reeks waarbij elk getal bv. ×2 of ÷3 is ten opzichte van het vorige.
Deze reeksen kunnen snel oplopen of juist snel kleiner worden, waardoor ze lastiger te herkennen zijn dan rekenkundige reeksen.
Zo herken je meetkundige reeksen:
- De verhouding tussen twee opeenvolgende getallen blijft gelijk.
- Het patroon zit in het vermenigvuldigen of delen, niet in vaste verschillen.
- De reeks versnelt of vertraagt zichtbaar.
Zo los je een meetkundige reeks op:
- Deel een getal door het vorige om te bepalen waarmee wordt vermenigvuldigd.
- Controleer of deze factor overal gelijk blijft.
- Pas die vermenigvuldiging toe op het laatste bekende getal om het volgende getal te vinden.
Een voorbeeld:
Voorbeeld van een meetkundige cijferreeks
Welk getal hoort op de plek van het vraagteken?
2, 6, 18, 54, ?
Klik op het juiste antwoord:
Tip voor meetkundige reeksen
Let op of het verschil tussen de getallen steeds groter of kleiner wordt. Als het verschil zelf ook verandert (bv. 2 → 6 → 18), dan is het geen vaste stap (zoals bij een rekenkundige reeks), maar een vermenigvuldigingspatroon. Denk dan direct aan een meetkundige reeks. Vervolgens kun je (zoals in de voorbeeldopgave hierboven) de verhoudingen tussen de verschillen uitrekenen en dit patroon toepassen op het vraagteken.
In een exponentiële reeks worden de getallen bepaald door een macht van een getal, zoals kwadraten (²) of derdemachten (³). Denk aan: 1 – 4 – 9 – 16 – 25, waarbij elk getal gelijk is aan 1², 2², 3², enzovoort.
Deze reeksen kunnen verwarrend zijn omdat ze in eerste instantie lijken op een meetkundige reeks vanwege snel toenemende verschillen.
Zo herken je exponentiële reeksen:
- De getallen ontstaan door een getal tot een macht te verheffen, zoals 2² (=4), 3² (=9) of 2³ (=8).
- Soms lopen de grondgetallen op (1², 2², 3²…), soms de exponenten (2¹, 2², 2³…).
- Het verschil tussen de getallen is niet constant, maar neemt toe in een onregelmatig en vaak versnellend patroon.
- Je herkent vaak bekende machten of getallen uit tafels en vierkantswortels, zoals 16 (=4²), 27 (=3³) of 81 (=9²).
Zo los je een exonentiële reeks op:
- Kijk of je alle getallen kunt herleiden tot een macht, zoals 2² (=4), 3³ (=27) of 5² (=25).
- Let op of er een duidelijk patroon zit in de grondgetallen of in de exponenten (bijv. oplopend: 2², 3², 4² of 2³, 2⁴, 2⁵).
- Zet de reeks voort door het volgende getal te berekenen op basis van dat patroon in machten.
Een voorbeeld:
Voorbeeld van een meetkundige cijferreeks
Welk getal hoort op de plek van het vraagteken?
1, 8, 27, 64, ?
Klik op het juiste antwoord:
Tip voor exponentiële cijferreeksen
Let op 'perfecte' getallen die je kent uit tafels of veelvoorkomende machten. Zie je getallen als 9, 16, 25, 27, 64, 81, 125 of 243? Dan is de kans groot dat je met kwadraten of derdemachten te maken hebt. Die komen zelden toevallig voor; vaak vormen ze de kern van een exponentiële reeks.
De tabel hieronder met de herkenbare machten (getallen 1 t/m 10) kun je als geheugensteuntje gebruiken.
| Getal | Kwadraat (²) | Derde macht (³) |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 729 |
| 10 | 100 | 1000 |
Bij een tweeledige reeks zit het patroon niet direct in de getallen zelf, maar in de verschillen tussen de getallen. Als je die verschillen op een rij zet, vormen ze vaak een aparte, herkenbare reeks, zoals een rekenkundige of meetkundige reeks.
Dit type opgave vereist gevorderd abstract redeneren: je moet een diepere laag herkennen voordat je het patroon kunt doorrekenen.
Zo herken je tweeledige reeksen:
- Het verschil tussen de getallen lijkt onregelmatig.
- Er lijken geen vaste stappen (rekenkundig, meetkundig of exponentieel) tussen de getallen zelf te zijn.
Zo los je een tweeledige reeks op:
- Schrijf de stappen tussen de getallen in de hoofdreeks op. Bijvoorbeeld bij: 2, 5, 10, 17 → Verschillen: +3, +5, +7
- Kijk of die verschillen zelf een patroon vormen. Herken je daar een vaste stap, een vermenigvuldiging of een andere logica?
- Gebruik het patroon in de verschillenreeks om de volgende stap te berekenen. In dit voorbeeld: volgende verschil is +9 → 17 + 9 = 26
- Controleer of het hele patroon klopt door terug te rekenen. Zo voorkom je dat je een vals patroon volgt.
Een aantal voorbeelden:
Voorbeeld 1 - Tweeledige cijferreeks
Welk getal hoort op de plek van het vraagteken?
3, 8, 15, 24, 35, ?
Klik op het juiste antwoord:
Het juiste antwoord is (C) – 48.
Uitleg:
Het verschil tussen de getallen neemt telkens toe met 2.
Daarom moet je bij het laatste getal in de reeks 13 optellen (11 + 2).
35 + 13 = 48
Het juiste antwoord is dus 48.
Voorbeeld 2 - Tweeledige cijferreeks
Welk getal hoort op de plek van het vraagteken?
2, 6, 12, ?, 30
Klik op het juiste antwoord:
Het juiste antwoord is (B) – 20.
Uitleg:
Er zijn twee manieren om deze cijferreeks te benaderen:
(1) De tussenstappen nemen steeds met 2 toe:
(2) Je kunt de getallen ook zien als producten van opeenvolgende getallen:
- 1 x 2 = 2
- 2 x 3 = 6
- 3 x 4 = 12
- 4 x 5 = 20
- 5 x 6 = 30
Het ontbrekende getal in de reeks is dus 20.
Voorbeeld 3 - Tweeledige cijferreeks
Welk getal hoort op de plek van het vraagteken?
0.1 | 0.4 | ? | 1.6 | 2.5
Klik op het juiste antwoord:
Het juiste antwoord is (C) – 0,9.
Uitleg:
Er zijn twee manieren om deze cijferreeks te benaderen:
(1) De tussenstappen nemen steeds met 0,2 toe:
(2) Je kunt de getallen ook als breuken bekijken:
- 0,1 = 1/10
- 0,4 = 4/10
- 0,9 = 9/10
- 1,6 = 16/10
- 2,5 = 25/10
De getallen in de teller (het bovenste/eerste getal van de breuk) zijn allemaal kwadraten: 1², 2², 3², 4², 5²
Het ontbrekende getal is dus 9/10 = 0,9.
Tip: zie je het patroon niet meteen? Probeer dan elk antwoordoptie in te vullen op de plek van het ontbrekende getal. Kijk vervolgens bij welke optie de verschillen tussen de getallen logisch toenemen – zoals in de uitleg hierboven.
Tip voor tweeledige reeksen
Als de hoofdreeks niet logisch lijkt, focus dan op de sprongen ertussen. Vaak blijkt daar het echte patroon te zitten en dat leidt je naar het juiste antwoord.
Een afwisselende reeks bestaat eigenlijk uit twee (of soms meer) patronen die elkaar afwisselen. In plaats van één doorlopende logica, moet je per om-en-om positie naar het patroon kijken. Vaak is er één patroon voor de even plekken en één voor de oneven plekken.
Zo herken je afwisselende reeksen:
- Het patroon tussen de opeenvolgende getallen is niet logisch of niet constant.
- Maar als je de getallen op even en oneven posities apart bekijkt, zie je twee duidelijke reeksen ontstaan.
Zo los je een meetkundige reeks op:
- Splits de reeks op in losse subreeksen. Kijk bijvoorbeeld alleen naar de oneven of de even posities.
- Zoek per deelreeks naar het patroon. Is het een optelling, vermenigvuldiging, alfabetische volgorde of iets anders?
- Pas beide patronen om-en-om toe om tot het juiste antwoord te komen.
Enkele voorbeelden:
Voorbeeld 1 van een afwisselende cijferreeks
Welke getallen horen op de plekken van de vraagtekens?
A3 | B4 | ? | ? | E7
Klik op het juiste antwoord:
Voorbeeld 2 van een afwisselende cijferreeks
Welk getal hoort op de plek van het vraagteken?
3 | 3 | 3 | 6 | 3 | 9 | 3 | ?
Klik op het juiste antwoord:
Het juiste antwoord is (C) – 12.
Uitleg:
Er zijn twee manieren om deze cijferreeks te benaderen:
(1) De reeks bestaat uit twee afzonderlijke deelreeksen, elk met een eigen patroon:
- De oneven posities (1e, 3e, 5e, ...) blijven steeds gelijk: 3
- De even posities nemen telkens toe met +3:
- 3 + 3 = 6,
- 6 + 3 = 9,
- 9 + 3 = 12
(2) Je kunt ook kijken naar de onderliggende bewerkingen:
De reeks volgt twee regels:
- De wiskundige bewerkingen tussen de getallen wisselen elkaar af in een vast patroon (bijvoorbeeld vermenigvuldigen en delen).
- Elke twee stappen wordt het getal waarmee je vermenigvuldigt of deelt met 1 verhoogd.
Het ontbrekende getal in de reeks is dus 12.
Voorbeeld 3 van een afwisselende cijferreeks
Welk getal hoort op de plek van het vraagteken?
6/3 | 5/4 | 4/5 | 3/6 | 2/7 | ?
Klik op het juiste antwoord:
Tip voor afwisselende reeksen
Lijkt de reeks onlogisch? Schrijf dan de getallen onder elkaar per positie. Noteer bijvoorbeeld de 1e, 3e, 5e getallen in één kolom, en de 2e, 4e, 6e in een tweede kolom ernaast. Zo splits je de reeks op in twee losse patronen en wordt het verschil vaak meteen zichtbaar.
Een Fibonacci-reeks is een reeks waarbij elk getal de som is van de twee voorgaande getallen. Bijvoorbeeld: 0, 1, 1, 2, 3, 5, 8, 13
Zo herken je fibonacci reeksen:
- De getallen lopen steeds sneller op.
- Er lijkt geen rekenkundig, meetkundig of exponentiëel patroon te zijn.
- Elk getal ontstaat door het vorige en het daarvoor liggende getal op te tellen.
Zo los je een fibonacci reeks op:
- Kijk naar de twee getallen voor het lege vakje.
- Tel ze bij elkaar op.
- Vul de som in als het ontbrekende getal.
Een voorbeeld:
Voorbeeld van een fibonacci cijferreeks
Welk getal hoort op de plek van het vraagteken?
3 | 5 | 8 | 13 | 21 | ? | 55
Klik op het juiste antwoord:
Tip voor fibonacci reeksen
Je kunt de reeks naar achteren controleren: trek twee opeenvolgende getallen van elkaar af. Kom je dan weer bij het vorige getal uit? Dan weet je dat je met een fibonacci reeks van doen hebt.
Een combinatiereeks is de moeilijkste soort cijferreeks en bevat meerdere verschillende bewerkingen, vaak in een vaste volgorde. Denk aan: +2, ×2, -3, +2, ×2, -3, enzovoort.
Deze reeksen lijken soms chaotisch, maar volgen gelukkig wel een regelmatig herhalend patroon.
Zo herken je meetkundige reeksen:
- Het verschil tussen de getallen is niet constant.
- Geen enkelvoudig patroon van alleen optellen, aftrekken, delen of vermenigvuldigen.
- Er lijkt sprake te zijn van een cyclus van meerdere bewerkingen die zich herhalen.
Zo los je een meetkundige reeks op:
- Kijk minimaal 3 of 4 stappen vooruit en schrijf de bewerkingen tussen de getallen op.
- Controleer of je een herhalend patroon ontdekt in de tussenstappen (bijv. +2, ×2, -1, dan opnieuw).
- Pas dat patroon toe op het laatste bekende getal om het volgende te vinden.
Een aantal voorbeelden:
Voorbeeld 1 van een combinatiereeks
Welk getal hoort op de plek van het vraagteken?
364 | 121 | 40 | 13 | 4 | ?
Klik op het juiste antwoord:
Voorbeeld 2 van een combinatiereeks
Welke getallen horen op de plekken van de vraagtekens?
12 | 13 | 14 | 10 | 11 | 14 | ? | ?
Klik op het juiste antwoord:
Het juiste antwoord is (D) – 8, 9.
Uitleg:
Er zijn twee manieren om deze cijferreeks te benaderen:
(1) De reeks bestaat uit drietallen die een vast patroon volgen:
- Het eerste getal van elk drietal is telkens 2 minder dan het eerste getal van het vorige drietal: 12, 10, 8.
- Het tweede getal is ook telkens 2 minder dan het tweede getal van het vorige drietal: 13, 11, 9.
- Het getal 14 komt steeds op de derde plek van elk drietal voor.
(2) Je kunt de reeks ook als volgt bekijken:
Elk drietal is onderling verbonden en volgt deze regels:
- Het tweede getal is steeds het eerste getal plus 1.
- Het derde getal is altijd hetzelfde: 14.
-
Het eerste getal van elk drietal is gelijk aan het tweede getal van het vorige drietal min 3.
Voorbeeld 3 van een combinatiereeks
Welk getal hoort op de plek van het vraagteken?
2 | 3 | 6 | 15 | 42 | ?
Klik op het juiste antwoord:
Voorbeeld 4 van een combinatiereeks
Welk getal hoort op de plek van het vraagteken?
0.5 | 3 | 28 | ? | 2778
Klik op het juiste antwoord:
Voorbeeld 5 van een combinatiereeks
Welk getal hoort op de plek van het vraagteken?
4 | 18 | 48 | 100 | ? | 294
Klik op het juiste antwoord:
Tip voor combinatiereeksen
Noteer alle tussenstappen afzonderlijk en kijk of ze zich herhalen. Let vooral op rekenvolgordes: soms komt eerst vermenigvuldigen, dan aftrekken, dan weer optellen. Herhaal je deze volgorde, dan valt de reeks vaak wel logisch te verklaren.
Waarom cijferreeksen oefenen met JobTestPrep?
Vind je cijferreeksen lastig en wil je je optimaal voorbereiden op je assessment? Koop dan ons cijferreeksen oefenpakket, inclusief:
- Honderden oefenvragen op elk niveau (MBO, HBO, WO)
- Tientallen realistische testsimulaties met tijdsdruk
- Uitleg bij elk antwoord en persoonlijk scoreoverzicht
- Alle soorten cijferreeksen voor verschillende testaanbieders (LTP, GITP, Assessio, Talent Q en meer)
- Direct online beschikbaar, te gebruiken op elk apparaat
Gratis cijferreeksen oefenen met 3 oefentests
We bieden drie gratis cijferreeksen test op verschillende niveaus aan (MBO, HBO of WO). Elke test heeft een tijdslimiet, net als bij een echt assessment. Na afloop zie je direct of je geslaagd bent. Je kunt bovendien per vraag de uitleg bekijken en leren van je fouten.
1. Gratis cijferreeksen test op MBO-niveau
In deze gratis test oefen je met 10 relatief makkelijke cijferreeksen. Slaag je voor de test? Dan ben je prima voorbereid voor cijferreeksen op MBO-niveau.
2. Gratis cijferreeksen test op HBO-niveau
In deze gratis test oefen je met 10 gemiddeld-moeilijke cijferreeksen. Slaag je voor de test? Dan ben je prima voorbereid voor cijferreeksen op HBO-niveau.
3. Gratis cijferreeksen test op WO-niveau
In deze gratis test oefen je met 7 moeilijke cijferreeksen. Slaag je voor de test? Dan ben je prima voorbereid voor cijferreeksen op WO-niveau.
Veelgestelde vragen over cijferreeksen
Cijferreeksen meten je logisch en analytisch denkvermogen. Werkgevers gebruiken ze om te beoordelen hoe snel en accuraat je patronen herkent, een belangrijke vaardigheid in veel functies.
Begin met de herkenning van veelvoorkomende soorten reeksen, zoals rekenkundig, meetkundig of afwisselend. Oefen daarna realistische tests onder tijdsdruk om snelheid en nauwkeurigheid te trainen.
Dat verschilt per test, maar meestal ligt de tijdslimiet tussen de 30 en 90 seconden per vraag. Omdat je onder tijdsdruk werkt, is het belangrijk dat je snel patronen herkent en efficiënt werkt. Oefening is daarbij essentieel.
Cijferreeksen zijn een vast onderdeel van veel capaciteitentests, vooral bij functies waarbij logisch en analytisch denken belangrijk is. Je komt ze onder andere tegen in:
- politietests
- de capaciteitentest van Defensie
- hbo-toelatingstoetsen
- selectieprocedures bij consultancybedrijven
- assessments van o.a. LTP, GITP, Assessio en Korn Ferry.
Nee, dat hangt af van de testaanbieder. Bij sommige assessments focussen ze alleen op andere onderdelen van een capaciteitentest, zoals figuurreeksen, diagrammen of analogieën. Lees altijd goed je uitnodiging door om te weten welke onderdelen jij moet oefenen.
Er is geen vaste norm, maar meestal geldt: hoe hoger je scoort ten opzichte van andere kandidaten, hoe beter. Als je bij de beste 25% hoort, zit je doorgaans goed.
Let op: sommige werkgevers gebruiken een vaste normscore, terwijl anderen je vergelijken met een referentiegroep. Hoe dan ook: goed oefenen maakt altijd verschil.
Ja, ChatGPT kan cijferreeksen analyseren en oplossen – vooral als het patroon logisch en eenduidig is.
Let wel: hoe complexer de reeks, hoe groter de kans dat ChatGPT fouten maakt. Daarom raden we altijd aan om te oefenen met door mensen samengestelde en gecontroleerde tests.
Onze oefenpakketten zijn ontwikkeld door experts en zorgvuldig getest, zodat je zeker weet dat je traint met realistische en betrouwbare opgaven.
Ja, er zijn verschillende apps en programma's waarmee je cijferreeksen kunt oefenen. Let er wel op dat de meeste apps vooral algemene reeksen aanbieden, vaak zonder tijdslimiet of uitleg. Wil je realistisch oefenen voor een assessment? Dan kun je beter kiezen voor een oefenpakket zoals dat van JobTestPrep met realistische vragen, tijdsdruk en uitleg per antwoord.
Soms bestaan cijferreeksen uit breuken in plaats van gehele getallen. Deze breuken volgen vaak een rekenkundig of meetkundig patroon, maar kunnen lastiger te herkennen zijn, zeker onder tijdsdruk.
Zo herken je cijferreeksen met breuken:
- De teller of noemer (of allebei) verandert volgens een bekend patroon.
- Het verschil tussen de breuken wordt kleiner of juist groter.
- De reeks kan ook bestaan uit decimalen die in werkelijkheid breuken voorstellen (zoals 0,5 – 0,25 – 0,125).
Zo los je cijferreeksen met breuken op:
- Zet de breuken eventueel om naar decimalen om het patroon sneller te herkennen.
- Kijk apart naar de teller en de noemer: verandert één van beide volgens een vaste stapgrootte of vermenigvuldigingsfactor?
- Gebruik kruiselings vermenigvuldigen of vereenvoudigen om de volgende breuk te voorspellen.
Tip: Zie je breuken met verschillende noemers? Reken ze eerst om naar gelijke noemers of decimalen. Dat maakt het makkelijker om een patroon te ontdekken.
